Faster RCNN系列
本文章粗略介绍了R-CNN系列的神经网络,并对前置知识做了详细的介绍与说明。
Nature Network
1.构成
由输入层、隐藏层、输出层、激活函数、损失函数组成。
- 输入层:接收原始数据
- 隐藏层:进行特征提取和转换
- 输出层:输出预测结果
- 激活函数:非线性变换
- 损失函数:衡量模型预测结果与真实值之间的差距
2.正向传播过程
基础的神经网络如下图所示,其中层1为输入层,层2为隐藏层,层3为输出层:
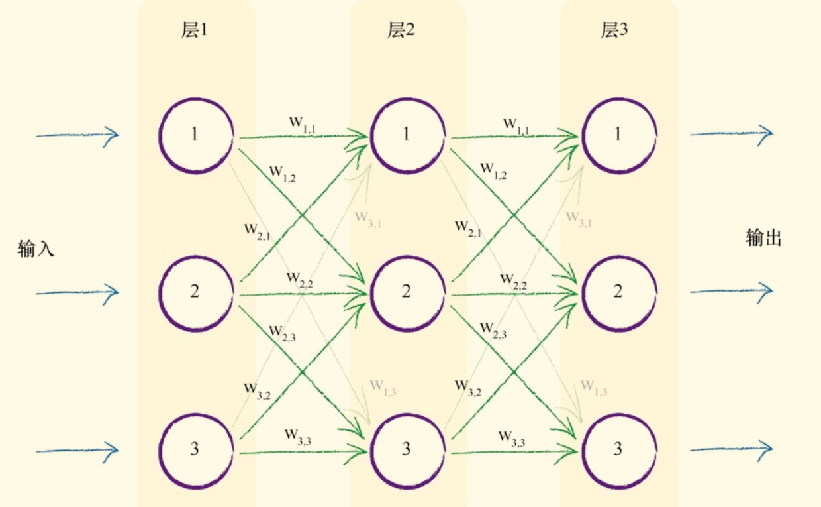
每一个圆圈代表了一个神经元,各层的神经元各自相连,如图中的绿色箭头。每一条相连的绿线上拥有起始设定好的权重。隐藏层的神经元后跟着激活函数,进行信号的转变。
对于每一层信号的输入输出,均有以下公式表达,X为此层的输入,O为此层的输出,一般输入层采用激活函数,即输入即为输出。
$$
X=W·Input\
O=sigmoid(X)
$$
$Input$ 为输入矩阵,此处以如下为例:
$$
Input =
\begin{bmatrix}
1.0\
0.5\
0.35
\end{bmatrix}
$$
$W$ 为权重矩阵,各层的权重各不相同
$$
W=
\begin{bmatrix}
w_{1.1} & w_{1.2} &w_{1.3}\
w_{2.1} & w_{2.2} &w_{2.3}\
w_{3.1} & w_{3.2} &w_{3.3}
\end{bmatrix}
$$
$sigmoid$ 为激活函数
$$
y=\frac{1}{1+e^{-x}}
$$
过程演示(3层)
1.输入层:由于输入层一般不使用激活函数,输入层的输出即为输入数据 $Input$。
2.隐藏层: 此层的输入为:
$$
X_{hidden}=W_{input2hidden} · Input=
\begin{bmatrix}
w_{1.1} & w_{1.2} &w_{1.3}\
w_{2.1} & w_{2.2} &w_{2.3}\
w_{3.1} & w_{3.2} &w_{3.3}
\end{bmatrix} · \begin{bmatrix}
1.0\
0.5\
0.35
\end{bmatrix}
$$
此层的输出为:
$$
O_{hidden} = sigmoid(X_{hidden})=\frac{1}{1+e^{X_{hidden}}}
$$
3.输出层: 输出层永远不使用激活函数,输出层的输出即为输入,输出层的输入为:
$$
X_{output} = W_{hidden2output}·O_{hidden}
$$
3.激活函数
上文使用的是$sigmoid$函数作为激活函数,还可以将其根据具体应用,更换为以下函数:
Sigmoid函数:将输入值压缩到0到1之间,常用于二分类问题
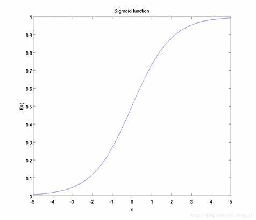
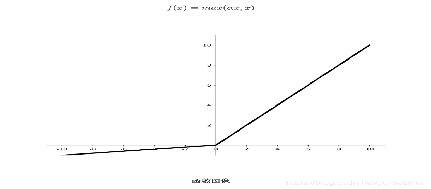
ReLU函数:将负值置为0,常用于深度神经网络中
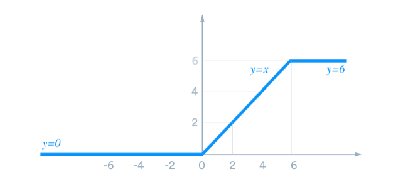
Tanh函数:将输入值压缩到-1到1之间,常用于回归问题
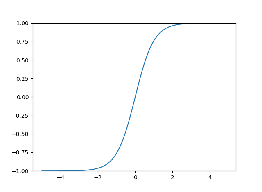
Leaky ReLU函数:对负值进行微小的缩放,避免梯度消失问题
4.反向传播过程
误差计算:目标值-实际值 $e_n = t_n - o_n$
下面以单个神经元返回误差为例:
对于最后输出的误差我们需要将他根据前一层的权重传播到前一层,以上面单个神经元的反向传播过程为例。传回1号神经元的误差为 $errors·\frac{w_1}{w_1+w_2}$ ,传回2号神经元的误差为 $errors·\frac{w_2}{w_1+w_2}$ 。
过程演示(3层)
下面我们把这个过程放到三层的神经网络中分析:

我们以第二层第一个神经元为例,分析误差传播到此的值。
$$
e_{hidden1} = e_{output1}·\frac{w_{1.1}}{w_{1.1}+w_{2.1}+w_{3.1}}+e_{output2}·\frac{w_{1.2}}{w_{1.2}+w_{2.2}+w_{3.2}}+e_{output3}·\frac{w_{1.3}}{w_{1.3}+w_{2.3}+w_{3.3}}
$$
接下来我们使用矩阵来表达这个麻烦的公式:
输出层误差:
$$
error_{output}=\begin{pmatrix}
e_1\
e_2\
e_3
\end{pmatrix}
$$
隐藏层误差:
$$
error_{hidden}=\begin{bmatrix}
\frac{w_{1.1}}{w_{1.1}+w_{2.1}+w_{3.1}} &\frac{w_{1.2}}{w_{1.2}+w_{2.2}+w_{3.2}} &\frac{w_{1.3}}{w_{1.3}+w_{2.3}+w_{3.3}}\
\frac{w_{2.1}}{w_{1.1}+w_{2.1}+w_{3.1}} &\frac{w_{2.2}}{w_{1.2}+w_{2.2}+w_{3.2}} &\frac{w_{2.3}}{w_{1.3}+w_{2.3}+w_{3.3}}\
\frac{w_{3.1}}{w_{1.1}+w_{2.1}+w_{3.1}} &\frac{w_{3.2}}{w_{1.2}+w_{2.2}+w_{3.2}} &\frac{w_{3.3}}{w_{1.3}+w_{2.3}+w_{3.3}}\
\end{bmatrix} · error_{output}
$$
去归一化:
$$
error_{hidden}=\begin{bmatrix}
w_{1.1} & w_{1.2} & w_{1.3}\
w_{2.1} & w_{2.2} & w_{2.3}\
w_{3.1} & w_{3.2} & w_{3.3}
\end{bmatrix} · error_{output} = w_{hidden2output}·error_{output}
$$
5.更新权重
下一步需要取得误差最小的权重作为最优权重,在此我们使用梯度下降的方法找到误差最小时的权重。
梯度下降:用于计算函数的最小值。随机起始点,通过导数的正负判断方向,朝着函数减小的方向,一步步增加x,并计算他的导数当导数为零或为设定范围内,取得最小值;否则继续增加。
在神经网络中由于x为权重矩阵,我们使用的梯度下降为多维梯度下降。
设定误差函数
在此例中我们使用 $E = (t_n-o_n)^2$
误差函数的斜率
$$
\frac{\partial E}{\partial w_{ij}}=\frac{\partial}{\partial w_{ij}}\sum_n(t_n-o_n)^2
$$
由于在这里 $o_n$ 仅取决于连接着的权重,所以误差函数的斜率可以改写为:
$$
\frac{\partial}{\partial w_{ij}}(t_n-o_n)^2
$$
根据导数的链式法则,我们改写斜率函数:
$$
\frac{\partial E}{\partial w_{ij}}=\frac{\partial E}{\partial o_n}\times \frac{\partial o_n}{\partial w_{ij}}=-2(t_n-o_n)\frac{\partial o_n}{\partial w_{ij}}
$$
我们再将$o_n$带入到此函数 $o_n=sigmoid(\sum_j w_{j,k}·o_j)$,$o_j$为前一层的输出,得到函数如下:
$$
斜率函数 = -2(t_n-o_n)\frac{\partial}{\partial w_{i,j}}sigmoid(\sum_j w_{jk}·o_j)
$$
我们对sigmoid函数进行微分:
$$
\frac{\partial sigmoid(x)}{\partial x} = sigmoid(x)(1-sigmoid(x))
$$
我们再把它放到斜率函数之中:
$$
斜率函数=-2·(t_n-o_n)·sigmoid(\sum_jw_{jk}·o_j)·(1-\sum_jw_{jk}·o_j)·\frac{\partial }{\partial w_{i.j}}(\sum_jw_{jk}·o_j)\
=-2·(t_n-o_n)·sigmoid(\sum_jw_{jk}·o_j)·(1-\sum_jw_{jk}·o_j)·o_j
$$
由于在此过程中我们只需判断斜率方向,我们可以把常数去除,即:
$$
斜率函数=-(t_n-o_n)·sigmoid(\sum_jw_{jk}·o_j)·(1-\sum_jw_{jk}·o_j)·o_j
$$
我们根据已有的关系对斜率在此修改:
- $(t_n - o_n)$ 为 $(目标值-实际值)$,即$e_i$
- $\sum_i w_{i,j}·o_i$ 为进入上一层的输入
- $o_i$ 为上一层的输出
$$
\frac{\partial E}{\partial w_{ij}}=-e_i \cdot sigmoid(\sum_i w_{ij}o_i)\cdot (1-sigmoid(\sum_i w_{ij}o_i))\cdot o_i
$$
更新权重
有了误差函数的斜率,我们就可以通过梯度下降的方式更新权重,其中$\alpha$为设定好的学习率:
$$
W_{new} = W_{old}-\alpha \frac{\partial E}{\partial w_{ij}}
$$
权重的矩阵变化
$$
\Delta w_{ij} = \alpha \cdot E_k \cdot o_k \cdot (1-o_k) \cdot o_j
$$
6.代码实现
神经网络代码应该由三部分组成:初始化函数、训练函数、查询函数
- 初始化函数:应该包含各层的节点数,学习率,随机权重矩阵以及激活函数
- 训练函数:应该包含正、反向传播,权重更新
- 查询函数:正向传播过程
1 | import numpy.random |
CNN(卷积神经网络)
1.构成
由输入层、卷积层、池化层、全连接层构成。
- 输入层:输入数据
- 卷积层:提取图像特征
- 池化层:压缩特征
- 全连接层:为输出准备,形同一维神经网络,下文不另起文笔描述
2.神经网络与CNN对比
左边为神经网络,右边为卷积神经网络。均采用的时较为简单的结构,卷积神经网络是对基础神经网络的延申,由一维扩展到三位空间,适用于对图像的操作。
3.卷积层
假设我们在输入一张$32 \times 32 \times 3$ 大小的图片进入CNN,我们在卷积层对他进行图像特征提取,输入图片输出特征图。首先我们需要设定以下参数作为卷积层的参数:
- 滑动窗口步长:卷积核移动的方式,通常使用1,即每进行一次卷积操作向右移动一个像素。
- 卷积核尺寸:常用 $3\times 3 ,11\times 11$等奇数尺寸。用于设定进行卷积操作的范围。
- 边缘填充:有时为了保证特征提取的结果(特征图)的大小,会在原图周围添加像素为零的点,再进行卷积操作。
- 卷积核个数:设定卷积核的个数。
卷积操作
其中卷积操作为需要卷积操作的范围内,对原图像的像素分别乘上卷积核对应内容并相加,得到结果,以红框即第一次卷积操作为例 结果为:
$$
01+20+41+10+31+50+301+120+32*1=64
$$
图片中展示的为单通道的卷积操作,由于我们输入的时RGB三通道的图片,我们需要3个卷积核对每一个通道进行卷积操作,再将三个通道相加得到特征图。
特征图尺寸
我们可以通过公式计算出最终得到的卷积结果的大小,其中H代表长,F代表卷积核,P代表Padding边缘填充,S代表步长:
$$
H_2 =\frac{H_1-F_H+2P}{S}+1\
W_2 = \frac{W_2-F_H+2P}{S}+1
$$
4.池化层
池化层是为了对特征图进行下采样(即压缩)而被使用的,池化有很多种方式,Max Pooling , Min Pooling , Average Pooling 等。在此我们仅解释Max Pooling操作,其余操作可依此类推:
Max Pooling:对取样范围内的值进行压缩,取范围内最大的值。
5.网络构建
在构成卷积神经网络时,在卷积层后增加激活函数,一般深度神经网络使用ReUL激活函数,每一个卷积层(conv)或全连接层(fc)称为神经网络中的一层。下面我们以一个四层神经网络为例:
6.常见的卷积神经网络
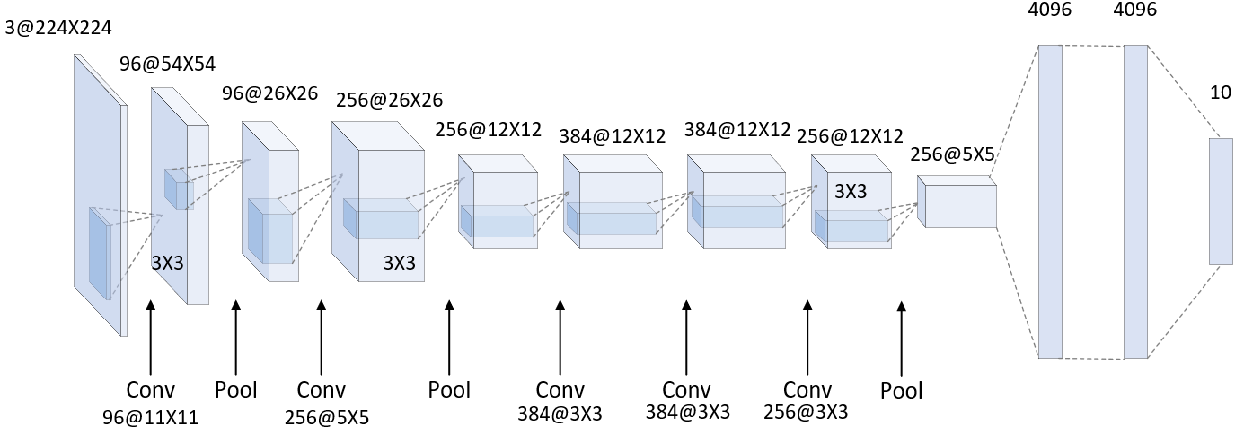
AlexNet*
AlexNet 为第一个深度神经网络,他一共有八层,其中五个卷积层和三个全连接层,卷积核的大小为 $11 \times 11$ ,0 padding。
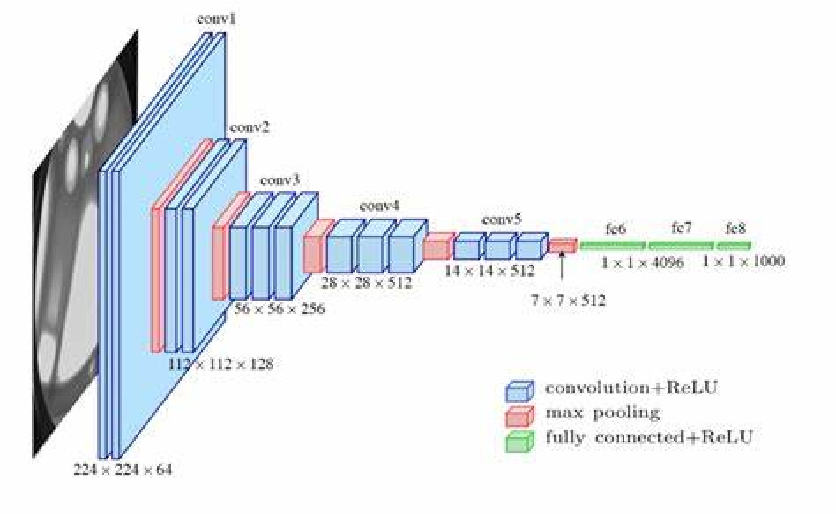
Vgg*
下列图中的结构为Vgg16,一共有16层,其中13个卷积层,三个全连接层,卷积核的大小为$3 \times 3$
ResNet*
由于添加更深层网络(大于20层)时,会出现精度下降的情况,导致20层以上的深度神经网络无法达到更好的性能。resnet网络则解决了这一问题,通过将上一层结果和本层卷积结果进行比较,取更优的网络作为我们传入下层的输入。

RCNN(区域神经网络)
RCNN的基本流程如下图所示,图片输入(1.)后通过区域选择算法取得候选框(2.),再将候选框通过图像缩放处理,统一到相同大小,传入深度神经网络中(论文中使用的AlexNet作为分类网络),最后通过支持向量机进行分类任务。
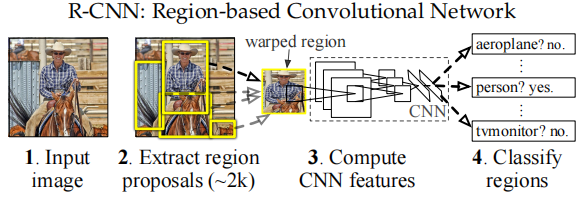
接下来我们一步一步学习具体的方法
1.区域选择算法*
在RCNN中我们选用selective search (选择性搜索算法)
- 生成区域集$R$,建立区域分割模型
- 计算$R$中每个相邻取悦的相似度$S = [S_1,S_2,S_3,\dots]$
- 找到相似度最高的两个区域,将他们合并成新集,添加到$R$中
- 从$S$ 中移除所有上一步中的有关子集
- 计算新集与所有子集的相似度
- 进行寻找相似度的步骤,除非$S$集合为空
相似度计算时需要分别计算颜色相似度、纹理相似度、尺寸相似度、填充相似度。最后乘权相加。
2.候选区域缩放
由于RCNN中采用的深度神经网络的输入是固定大小的,而通过选择性搜索后的2000个proposal大小并不相同,所以我们需要通过某种算法对proposals的图像大小进行更改使得propsals的大小符合深度神经网络的输入要求。
通过比较多种图像缩放的技术,我们采用各向异性图像缩放(图像拉伸)的方式对神经网络的输入进行修正。

A为选择性搜索算法的结果,BC为padding与否的正方形选框,D为各向异性图像缩放技术,上图为0 padding,下图为16 padding。
3.整体流程
- 训练分类网络(AlexNet)
- 模型迁移:去除AlexNet中的FC,将类别修改为需要分类的类别数(论文中为20)
- 特征特区:分为候选区域提取、图像缩放、分类网络图像特征提取
- 训练SVM分类器:每一个类别对于一个SVM,训练N+1(增加背景)
- 回归定位:回归经过精修后的候选框位置,利用线性回归模型判定框的精确度
4.存在缺点
- 候选框选择算法耗时严重
- 重叠区域特征重复计算
- 分步骤执行,过程繁琐
SPP-Net
SPP-Net是对于RCNN的优化,对于图像首先进行图像特征提取,对于原图像进行selective search,截取feature map中对应的候选区域作为propsals,再建立 Spatial Pyramid Pooling (池化金字塔)调整最终的输出,传入FC层,最终通过SVM进行图像分类。
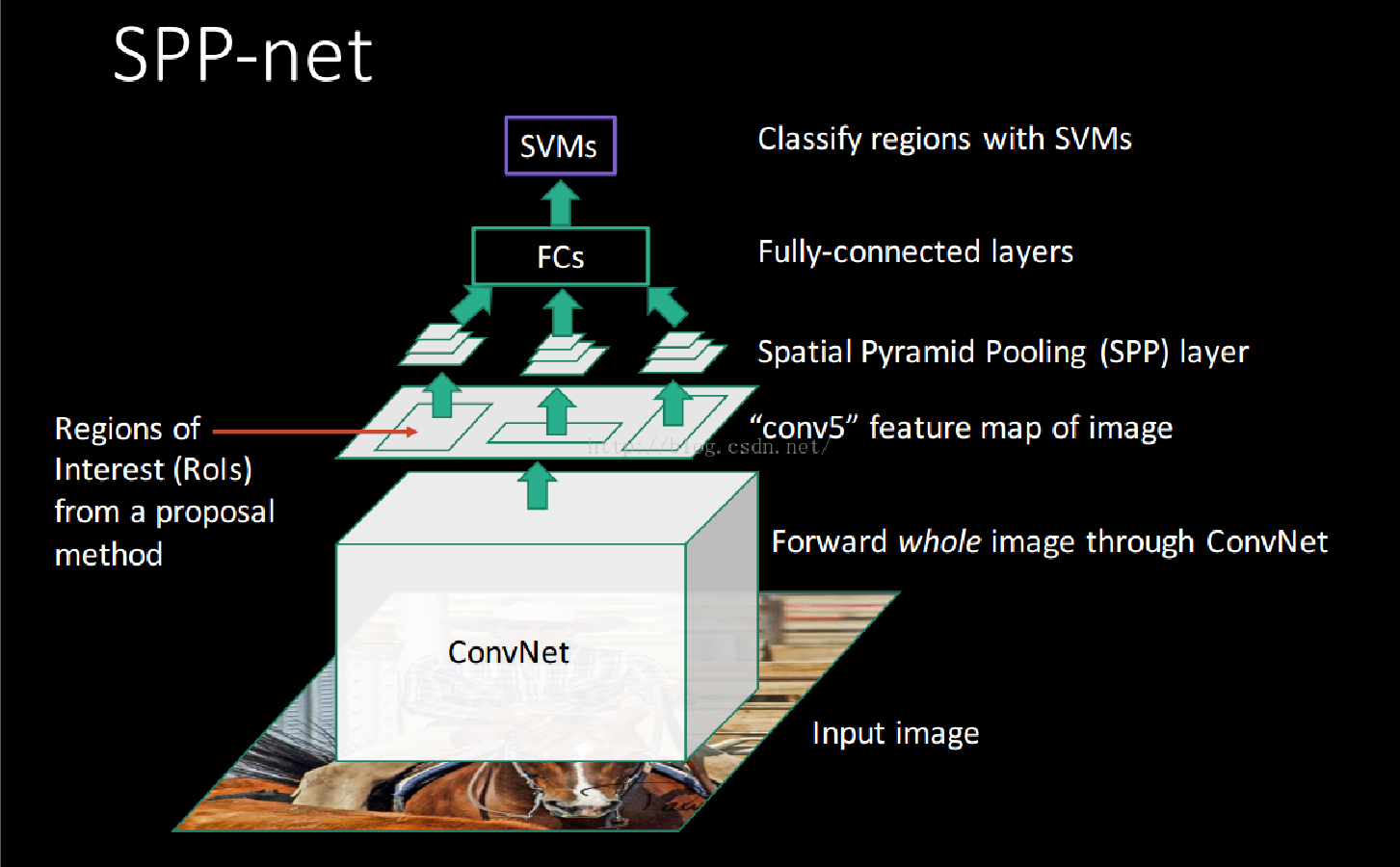
Spatial Pyramid Pooling
通过将输入的feature map 分别分成 $44$ $22$ $1*1$ 网格,在对网格进行 Max Pooling 操作,再把所得的结果拼接在一起就形成了相同大小的特征向量了,具体流程如下图所示:
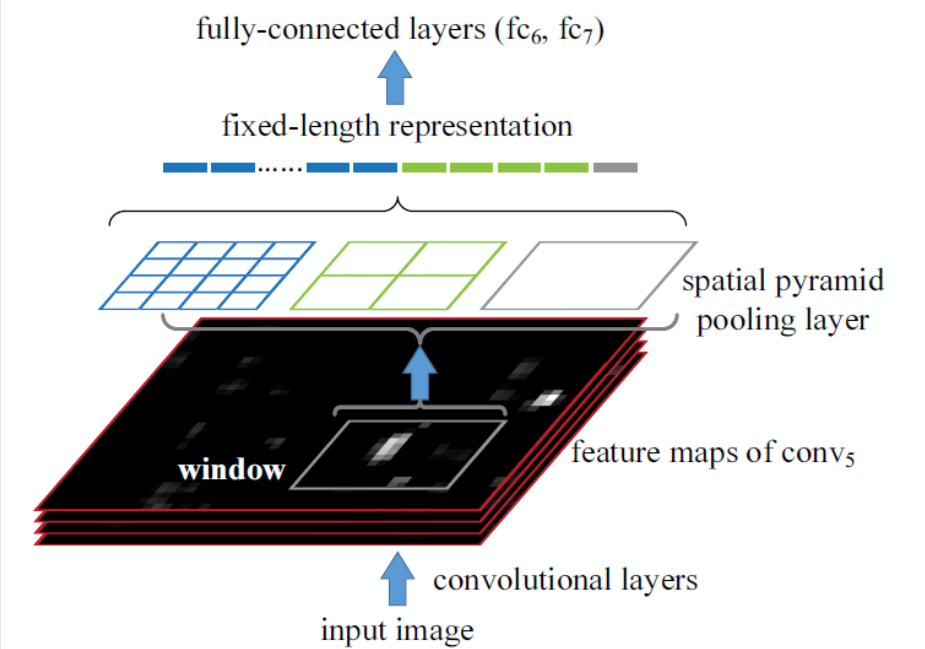
Fast R-CNN
Fast R-CNN 是结合SPP-Net 对于RCNN的改进,将SPP-Net中的Spatial Pyramid Pooling结构调整为 RoI Pooling结构,只是用SPP中的一层。
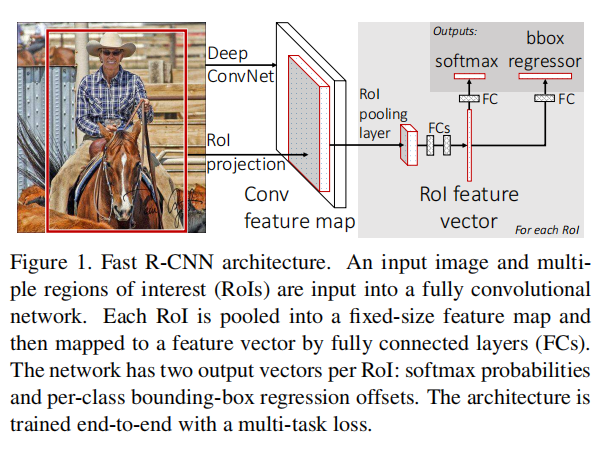
输入图片后,同时进行选取propsals和提取feature map 操作在进行RoI pooling 操作将特征图传入全连接层,在对其进行分类和回归任务。
Faster R-CNN
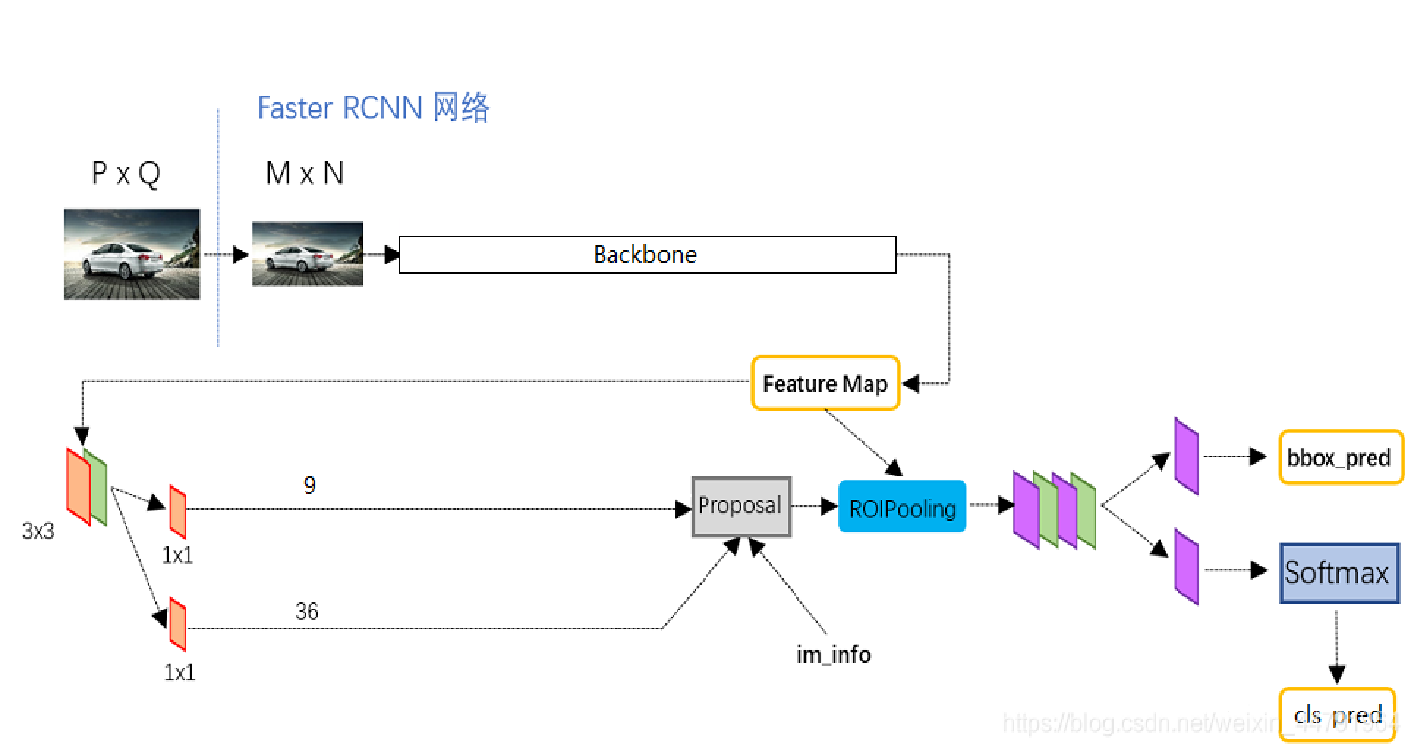
Faster R-cnn 是对Fast R-cnn的更新,采用了RPN区域建议网络以及Fast RCNN中提出的RoI Pooling层,实现了端到端的检测。
RPN网络
为了提升传统的selecive search 方法的速率,Faster R-CNN中使用一个小的神经网络结构优化了目标框取,即RPN网络,接下来我们分点介绍RPN网络的功能结构。
预选框:我们对每一个点进行Anchor生成,一个点对应设定好的九个Anchor框作为预选框
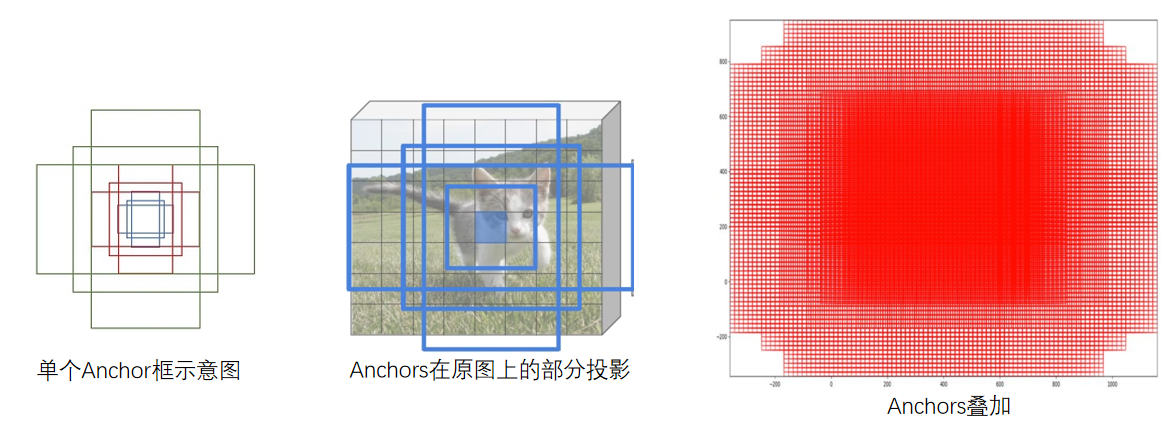
前后景区分:我们采用二分类的方法区分前后景
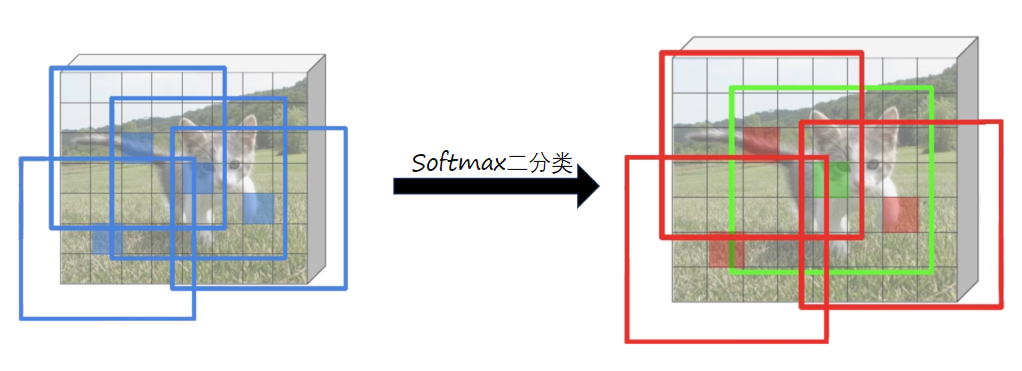
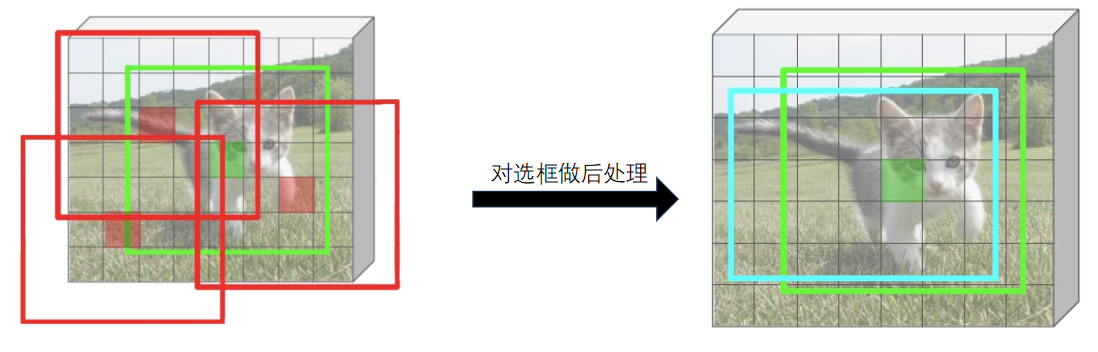
选框后处理:我们需要对于选出的前景框进行处理,使得更接近目标框