软件设计知识
现在是2024年的2月13日,一月份购置了《软件设计师教程》一书,想着单单看着总会遗忘很多知识点,于是有了这一篇文章。原本的打算是做成零碎的文章,但零碎的知识点于平时别的碎碎念会产生混乱,于是今日将他们整合到一起,同时将之前写过的相关内容一并放于此地。这一篇文章会慢慢更新,逐步完善下去,希望不会再次发生弃坑的恶习吧~
[TOC]
计算机系统硬件的基本组成
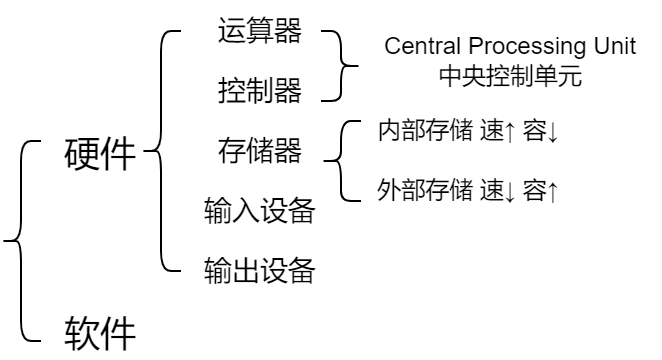
计算机系统是由 软件和硬件 构成的。硬件系统由 运算器、控制器、存储器、输入设备、输出设备 五大部件组成。运算器、控制器等部件被集成在一起统称为中央处理单元 Central Processing Unit 。输入和输出设备合称为外部设备。存储器分为内部存储器和外部存储器,内部存储器 速度高、容量小,一般用于临时存放程序、数据及中间结果,外部存储器 速度慢、容量大,长期保存程序和数据。
中央处理单元
中央处理单元 CPU 是计算机系统的核心不见,它负责 获取 程序指令、对指令进行 译码 并进行 处理 。
CPU的功能
- 程序控制 :控制程序执行的 顺序
- 操作控制 :发出 操作信号 至对应部件并使对应部件执行程序
- 时间控制 :控制操作信号的 出现 时间、保持 时间和出现的 时间顺序
- 数据处理 :算术和 逻辑运算
- 中断(异常)响应
CPU的组成
CPU主要由 运算器 、 控制器 、 寄存器组 和 内部总线 等部件组成。
运算器
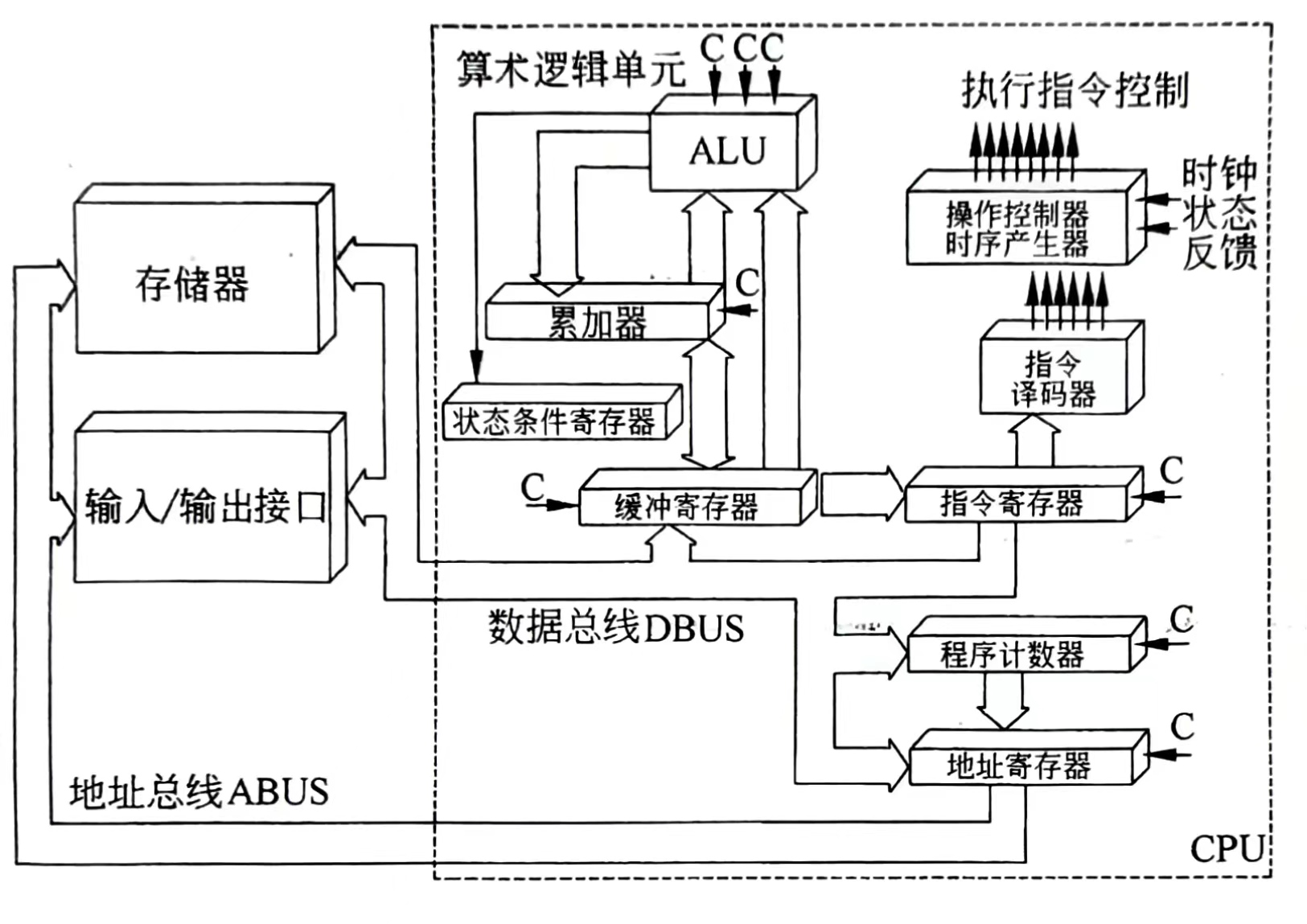
运算器由 算术逻辑单元(Arithmetic and Logic Unit, ALU)、累加寄存器、数据缓冲寄存器 和 状态条件寄存 等组成。它是数据加工处理部件,用于完成计算机的各种算术和逻辑运算。
- 算术逻辑单元 ALU 处理数据
- 累加寄存器 AC 提供工作区,存放结果
- 数据缓冲寄存器 DR 数据暂存,速度缓冲,单AC结构兼做操作数寄存器
- 状态条件寄存器 PSW 保存状态标志和控制标志
控制器
保证程序正确执行,且能够处理异常事件。一般包括指 令控制逻辑 , 时序控制逻辑 , 总线控制逻辑 和 终端控制逻辑 几个部分。
指令控制逻辑要完成取指令、分析指令和执行指令的操作,其过程分为取指令、指令译码、按指令操作码执行、形成下一条指令地址 等步骤。
- 指令寄存器 IR 指令暂存,指令从内存中取出放入DR中,再从DR通过总线到达IR。
- 程序计数器 PC 寄存信息、计数,指向下一条地址
- 地址寄存器 AR 保存当前访问的指令
- 指令译码器 ID 分析解释操作码字段,发出控制信号
多核CPU
核心,又称内核,使CPU最重要的组成部分。CPU所有的 计算、接收/存储命令、处理数据 都由 核心 执行。

单核多线程CPU是 交替地转换执行 多个任务。多核在理论上则是在 任何时间内 每个核执行各自的任务,不存在交替问题。因此多核速度更快。注:采用了 Intel超线程技术 的单核可以视为是双核,但 比不上 实际双核的性能。
数据表示
仅在数值为 负 时,各种码的相互转换 如下图 。当数值为 正 时各码 相同 。

数值0的原码表示有两种形式:$[+0]_原=0 0000000$ ,$[-0]_原=1 0000000$
浮点数表示时采用 IEEE754 标准,$N = 2^E \times F$ , E为解码,F为尾数。浮点数所能表示的 数值范围 由 阶码 决定,所表示数值的 精度 则是由 尾数 决定。为了充分利用尾数来表示更多的有效数字,通常采用 规格化浮点数 。将尾数的绝对值限定在区间[0.5,1]。
IEEE754标准,一般单精度浮点个参数需牢记
| 数符 S(1位) | 阶码 E (8位) | 尾数 M (23位) |
|---|
| 参数 | 单精度浮点 | 双精度浮点 | 扩充精度浮点 |
|---|---|---|---|
| 浮点数字长 | 32 | 64 | 80 |
| 尾数长度P | 23 | 52 | 64 |
| 符号位S | 1 | 1 | 1 |
| 指数长度E | 8 | 11 | 15 |
| 最大指数 | +127 | +1023 | +16383 |
| 最小指数 | -126 | -1022 | -16383 |
| 指数偏移量 | +127 | +1023 | +16383 |
| 可表示的实数范围 | $10^{-38}-10^{+38}$ | $10^{-308}-10^{+308}$ | $10^{-4932}-10^{+4932}$ |
IEE754对阶码采用偏移量表示,单精度浮点数 偏移值为 127 ,双精度浮点数的偏移值为1023,临时浮点数的偏移值为16383。计算阶码时需要在 阶数的原码上加上偏移量,以单精度浮点数为例阶数为7,则$[7]_原$ = 0000 0111 ,阶码为 $[7]_原+[偏移量]_原$= 0000 0111 + 0111 1111 = 1000 0110
- 规格化的值 :阶码部分的二进制值不全为0或1。表示的是规格化的值。
- 非规格化的值 :当阶码部分的二进制全为0时,所表示的数是非规格化的。表示数值0,或是哪些非常接近0的数
- 特殊值 :当阶码部分的二进制权威1时,符号位为0表示正无穷,为1表示负无穷
校验码
- 合法编码 :用于传送数据。
- 错误编码 :不允许在数据中出现的编码。
- 码距 : 任意两个合法编码之间至少有多少个二进制位不同。
奇偶校验码
奇偶校验 Parity Codes ,通过在编码中加入一位校验位来使编码中的 1的个数为奇数 (奇校验),或者使1的个数为偶数 (偶校验)
| 数据 | 偶校验编码C | 奇校验编码C |
|---|---|---|
| 1010 1010 | 1010 1010 0 (偶数个1) | 1010 1010 1 (奇数个1) |
| 0101 0100 | 0101 0100 1 | 0101 0100 0 |
| 0111 1111 | 0111 1111 1 | 0111 1111 0 |
| 1111 1111 | 1111 1111 0 | 1111 1111 1 |
海明码
海明码 Hamming Code 在数据为之间的特定位置上插入k个校验码,通过扩大码距来实现检错和纠错。假设k个校验位为 $P_k,P_{k-1},…,P_1$,n个数据位为 $D_{n-1},D_{n-2},…,D_{0}$ ,对应的海明码为 $H_{k+n} … ,H_1$
- $P_i$ 在海明码的第 $2^{i-1}$ 位置,数据位则依序从低到高占据海明码的剩余位置
- 海明码中的任何一位都是由若干个校验位来校验的。其对应关系如下:被校验的海明位的下标等于所有参与校验该位的校验位的下标之和,而校验位由自身校验。
| 海明码 | 海明码的下标 | 校验位组 |
|---|---|---|
| $H_1(P_1)$ | 1 | $P_1$ |
| $H_2(P_2)$ | 2 | $P_2$ |
| $H_3(D_0)$ | 3=1+2 | $P_1,$$P_2$ |
| $H_4(P_3)$ | 4 | $P_3$ |
| $H_5(D_1)$ | 5=1+4 | $P_1,P_3$ |
| $H_6(D_2)$ | 6=2+4 | $P_2,P_3$ |
| $H_7(D_3)$ | 7=1+2+4 | $P_1,P_2,P_3$ |
| $H_8(P_4)$ | 8 | $P_8$ |
其中校验位的生成由校验位组的异或和决定:
$P_1 = D_0\oplus D_1 \oplus D_3$
$P_2 = D_0\oplus D_2\oplus D_3$
$P_3 = D_1\oplus D_2 \oplus D_3$
循环冗余校验码
循环冗余校验码 Cyclic Redundancy Check 广泛应用于数据通信领域和磁介质存储系统中。利用生成多项式为k个数据为产生r个校验位来进行编码。左边信息码k位,右边校验码n-k位。故又称(n,k)码。
数据结构
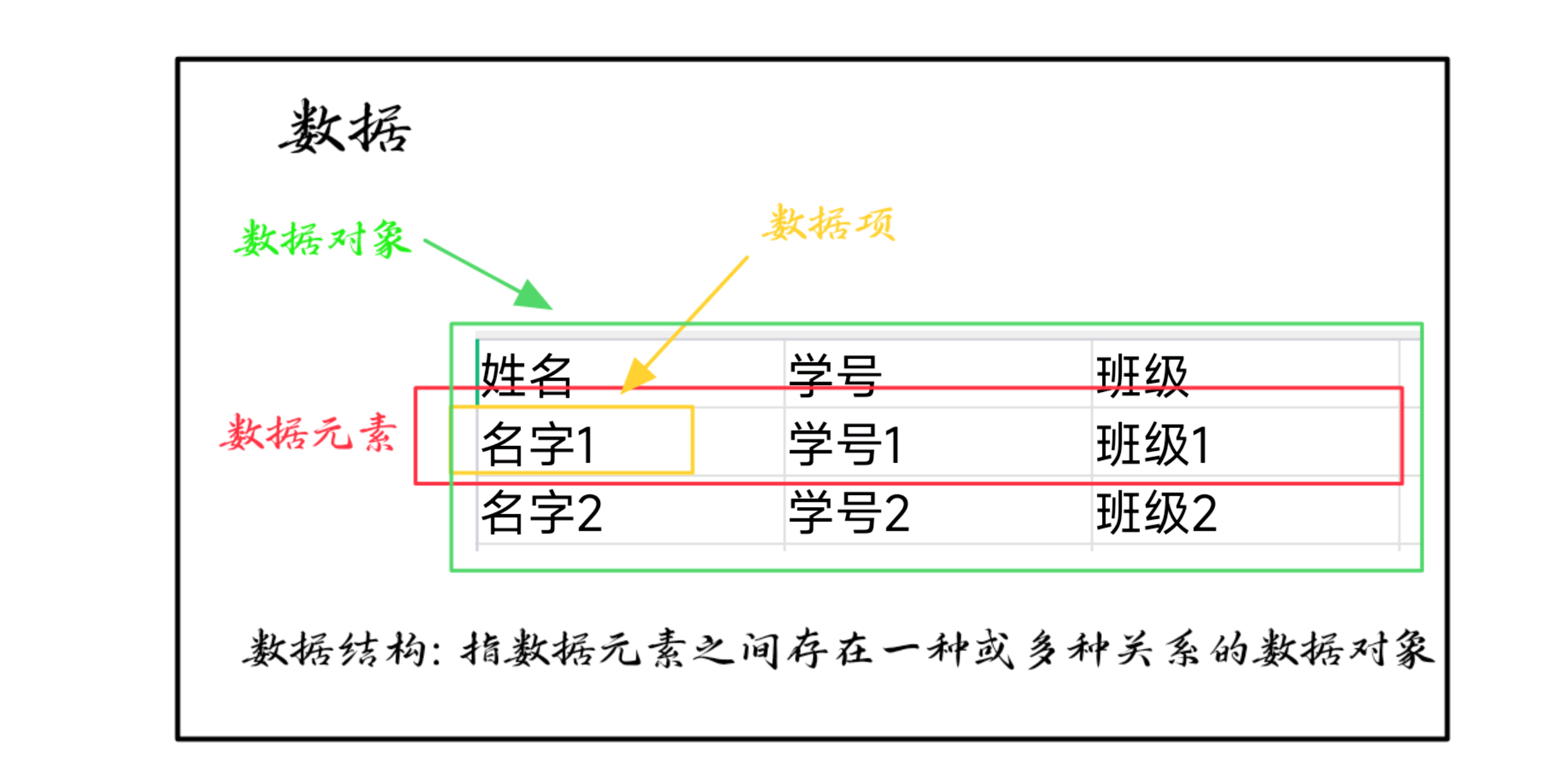
- 数据: 所有能被 输入到计算机 中,且能 被计算机处理 的符号的集合,是计算机操作对象的总称
- 数据元素: 数据中的一个个体,通常作为一个整体考虑和处理。也被称为元素、结点、记录。
- 数据项: 具有 独立含义 的最小标识单位,也称字段或域。
- 数据对象: 具有 相同特性 的元素的集合。
- **数据结构: ** 指以某种内在联系将数据元素组成一个数据对象。
基本形式
$$
Data_Structure = (D,R) \
其中D为数据元素的有限集合,R为D上关系的有限集
$$
基本结构
集合结构:元素关系松散
线性结构:元素之间有 一对一关系
树形结构:元素之间有 一对多关系
图形结构:元素之间有 多对多关系
逻辑结构:是对数据元素之间存在的逻辑关系的描述。
物理结构:又称存储结构,是指在计算机中的表示和实现。
- 顺序存储
- 链式存储
- 索引存储
- 哈希存储
抽象数据类型
抽象数据类型(ADT)是指一个数学模型以及定义在该模型上的一组操作。通常如下表示:
1 | ADT 抽象数据类型名{ |
算法
算法是一个有穷的规则集合,这些规则为解决某一特定任务规定了一个 运算序列 。简单来说算法是解题的步骤。
算法描述方法
- 自然语言:英语、汉语、日语等自然演化的语言
- 程序设计语言
- 流程图:传统流程图或者N-S结构图
- 伪语言:伪代码,介于自然语言与程序设计语言之间。
- PAD图:问题分析图,较为新颖,可以深入了解
特性
- 有穷性:必须在有穷步之后正常结束
- 确定性:每一步必须有确切的定义,无二义性
- 可行性:每一条指令确实可行
- 输入:零个或多个
- 输出:一个或多个
算法分析
所需要的时间却决于下列因素:
- 硬件速度
- 书写的程序语言:实现语言越高级,执行效率越低
- 编译程序所生成目标代码的质量
- 问题规模
空间复杂度
指程序运行从开始到结束所需的存储量。包括两部分
- 固定部分:主要包括程序代码、常量、简单变量、定长成分和结构变量所占空间
- 可变部分:与算法在某次执行中处理的特定数据的大小和规模有关
时间复杂度
指程序运行从开始到结束所需要的时间。针对算法中语句执行次数做出估计。首先计算算法语句对应的语句频度,以下列c语言代码为例:
1 | for(i=0;i<n;i++){ n |
总执行次数为
$$
T(n)=2n^3+2n^2+n
\
算法的时间复杂度记为:T(n)=O(f(n))
$$
我们仅用最大次数表示算法的时间复杂度,即上文的代码时间复杂度为$T(n)=O(n^3)$
常用的世间法咋读频次计数:常数型$O(1))$ ,线性型$O(n)$ ,平方型$O(n^2)$ ,立方型$O(n^3)$ ,指数型$O(2^n)$ ,对数型$O(\log _2 n)$ ,二维型$O(n\log _2 n)$ 。
基本算法策略
穷举法
穷举法,或称枚举法、暴力破解法,是一种针对密码的破译方法,即将密码进行逐个推演指导找出真正的密码为止。
应用:求质数、百钱买百鸡
递推法与迭代法
递推是计算机数值计算中对的一个重要算法,将复杂的运算划分为可以重复操作的若干个简单运算。
典型应用:Fibonacci
分治法
将一个难以直接解决的大问题,分割 成一些规模较小的相同问题,以便各个击破。适用于规模缩小到一定程度可以解决、具有最优子结构性质、子问题的解可以合并为该问题的解、子问题相互独立的问题中。下面介绍分治法的步骤:
在每一层递归上都有三个步骤
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题
- 解决:若子问题规模较小而容易被解决则直接解,否则再继续分解为更小的子问题
- 合并:将已经求解的子问题的解逐步合并为原问题的解
贪心算法
不追求最优解,只希望得到较为满意解的方法。一般可以快速得到满意的答案。常以当前情况为基础作最优选择,而不考虑各种可能的整体情况,所以贪心算法不需要回溯
动态规划
引入一个数组,不管他们是否对最终解有用,把所有子问题的解存放于该数组中。基本思想为:把求解的问题分成许多阶段或者子问题,然后按照顺序求解各阶段或子问题,记录每个阶段决策得到的觉果序列。最后阶段的解就是初始问题的解。
适用问题:最优子结构(必须有),无后向性,子问题重叠性质
编译原理
词法分析/扫描(Scanning)
从左向右逐行扫描源程序的字符,识别出各个单词,确定 单词的类型 。将识别出的单词转换成统一的 机内表示 , 词法单元(token)形式:
1 | token:<种别码, 属性值> |
| 单词类型 | 种别 | 种别码 |
|---|---|---|
| 关键字 | program, if , else… | 一词一码 |
| 标识符 | 变量名,数组名,记录名… | 多词一码 |
| 常量 | 整型,浮点型,字符型… | 一型一码 |
| 运算符 | 算术、关系、逻辑 | 一词\一型一码 |
| 界限符 | ; ( ) = { } … | 一词一码 |
语法分析( parsing)
语法分析器 (parsing) 从此法分析器输出的token序列中 识别出各类短语 ,并构造语法分析树。
1 | position = initial + rate * 6; |
语义分析
收集标识符的属性信息
种属 (kind)
类型 (type)
存储位置,长度
值
作用域
参数和返回值信息
语义检查
- 变量或过程未经声明就使用
- 变量或过程名重复声明
- 运算分量类型不匹配
- 操作符与操作数之间的类型不匹配
- 数组下标不是证书
- 对非数组变量使用数组访问操作符
- 对非过程名使用过程调用操作符
- 过程调用的参数类型或数目不匹配
- 函数返回类型不匹配
中间代码生成
- 三地址码 (Three-address Code)
- 三地址码由类似汇编语言的指令序列组成,每个指令最多有三个操作数
- 语法结构树/语法树 (Syntax Trees)
目标代码生成
- 目标代码生成以源程序的中间表示形式作为输入,并把它映射到目标语言
- 目标代码生成的一个重要人物是为程序中使用的变量 合理分配寄存器
代码优化
- 为改进代码所进行的 等价程序变换 ,使其 运行得更快 , 占用空间更少 。
语言和文法
字母表(Alphabet)
- 字母表$\Sigma$ 是一个有穷符号集合
- 字母表的 乘积 : $\Sigma_1 \Sigma_2 = {ab|a\in\Sigma_1,b\in \Sigma_2}$
- 字母表的 n次幂 : $\Sigma^n = \Sigma^{n-1}\Sigma$
- 字母表的 正闭包 : $\Sigma^+ = \Sigma^1U\Sigma^2U\Sigma^3…$
- 字母表的 克林闭包 : $\Sigma^* = \Sigma^0 U \Sigma^+$
串(String)
- 串是字母表中 符号的 一个 有穷序列
- 串s的 长度 通常记作 |s| ,指其中符号的个数
- 空串 是长度为0的串,用 $\epsilon$ 表示
- 串的连接 : x = dog , y= house , xy = doghouse
- 串的幂运算 :若s = ba, 有 $s^1=ba, s^2=baba, s^3=bababa…$
文法
$$
G=(V_T,V_N,P,S)
$$
$V_T:$ 终结符集合 , 终结符(terminal symbol) 是文法所定义的语言的 基本符号 ,有时也称为token
$V_N:$ 非终结符集合 ,非终结符(nonterminal) 是用来表示语法成分的符号,也称语法变量
$P:$ 产生式集合,产生式(production) 描述了将终结符和非终结符组合成串的方法
- 一般形式:$\alpha$->$\beta$
- 产生式的简写:对一组有相同 左部 的产生式可以简记为:$\alpha$ -> $\beta_1 | \beta_2 | \beta_3…$ ,右部可称为 $\alpha$ 的候选式
$S:$ 开始符号
推导(Derivations)和归约(Reductions)
- 推导: 用产生式的左部替换产生式的左部
- 归约: 推导的逆运算
文法分类:
- 0型文法: 无限制文法,左部至少包含一个非终结符
- 1型文法: 上下文有关文法,左部符号的个数不准多于右部符号。不包含空产生式
- 2型文法: 上下文无关文法,左部不能出现终结符
- 3型文法: 正则文法(RG)
- 右线性文法: $A$->$w B$ 或 $A$->$w$
- 左线性文法: $A$->$B w$ 或 $A$->$w$
设计原则
为了提高软件的可维护性、可复用性,增加软件的可扩展性和灵活性,在面向对象编程的过程中我们需要遵守以下六条原则。
开闭原则
定义: 编写的代码需要对 扩展开放 对 修改关闭 ,实现 热插拔 的效果。
例:在编写不同皮肤类的时候, 不能对抽象类进行修改 ,而是开放扩展功能,通过编写子类实现不同效果。

里氏代换原则
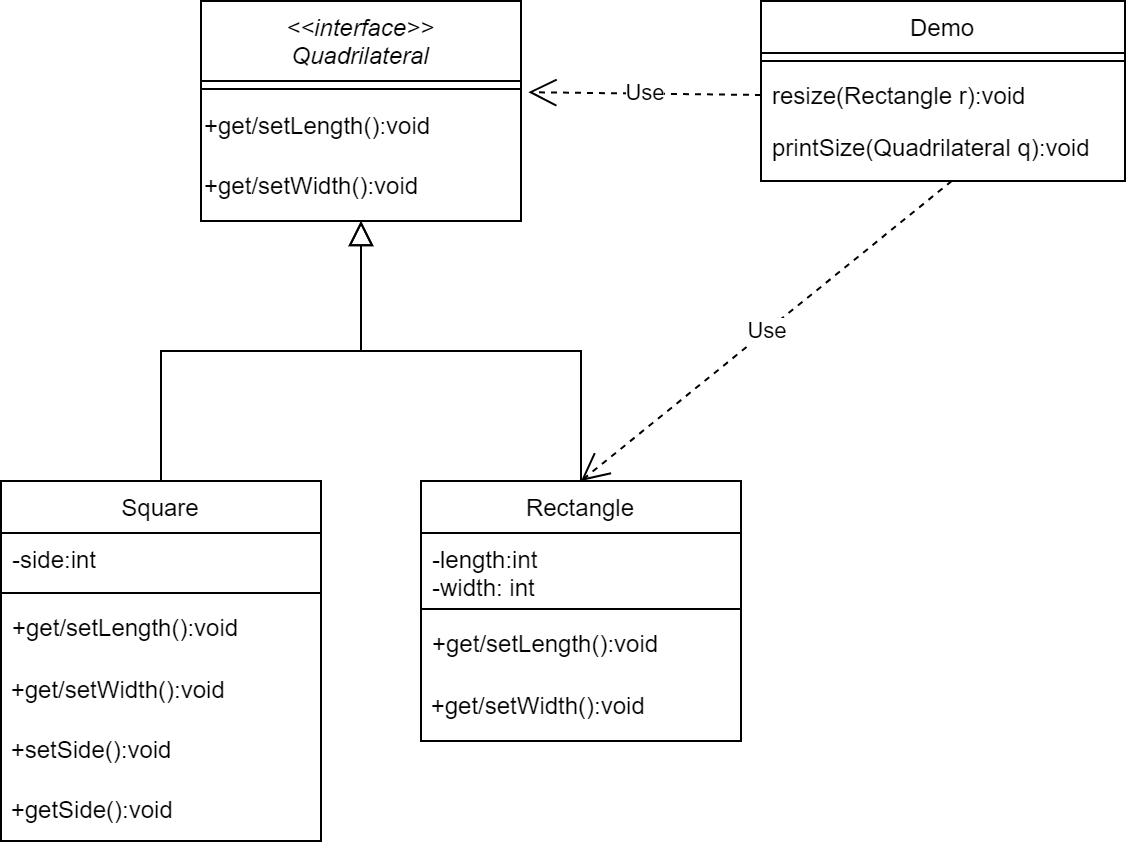
定义: 任何 基类 可以出现的地方, 子类 一定可以出现。即,子类 可以扩展 父类功能,但 不能改变 原有的功能,尽量 不重写 父类的方法。 多态频繁的程序出错的概率很大。
例:正方形若直接继承长方形,则需要修改其父类的方法。正确的方式应该是将两者抽象出一个共同的接口,用于实现。
依赖倒转原则
定义: 高层模块 不应该 依赖低层模块,两者都应该 都依赖其抽象 。抽象不应该依赖于细节,细节应该依赖抽象 。
若A类是高层模块,B类是低层模块,那么他们应该有如下关系:

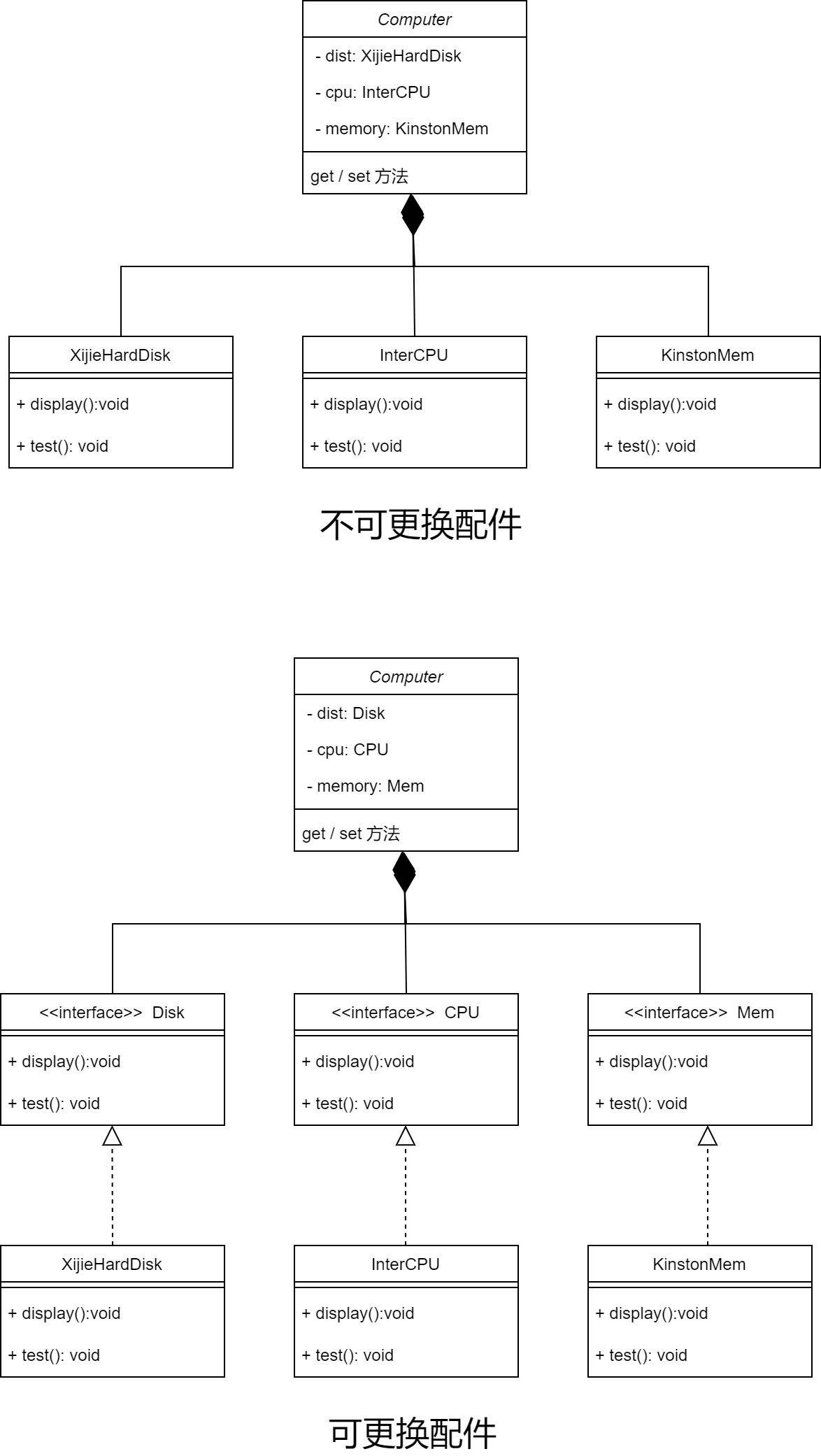
例:若要组装一个电脑类,若实现的是各个部件组合于此类,则会出现不能进行具体更改的情况,应该实现将他们的接口组合于此类的效果,再实现各个接口。
接口隔离原则
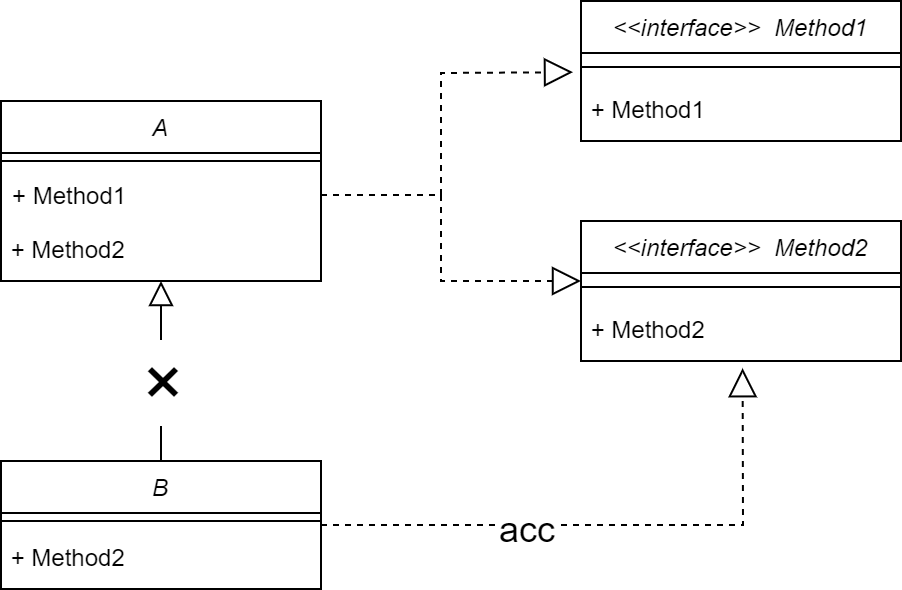
定义: 客户端不应该依赖于他不使用的方法。一个类对另一个类的依赖应该建立在最小的接口上。
列:若B类想要实现A类中的方法2,则不应该继承A类,而是实现方法2的接口。
迪米特法则
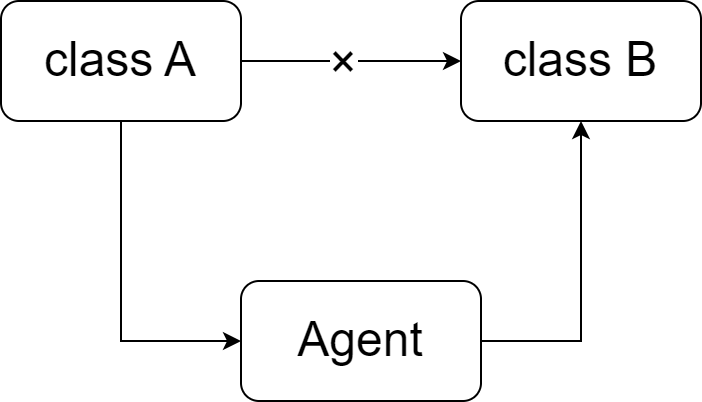
定义: 又称 最少知识法则,Talk only to your immediate friends and not to strangers. 如果两个软件实体 无需通信 ,那么就 不应当 发生直接的相互调用,可通过 第三方转发调用 。(降低耦合)
friend: 当前对象 本身 ,当前对象的 成员对象 ,当前对象 所建的对象 ,当前对象的 方法参数 。
合成复用原则
定义: 尽量先使用组合或聚合等关联关系实现某一个实例,其次才考虑继承。通常类的复用分为 继承复用 和 合成复用
- 继承复用: 简单、易实例化
- 破坏类的封装性
- 子类与父类的耦合度高
- 限制复用的灵活性
- 组合/聚合复用: 将已有对象进行组合
- 维护了类的封装性
- 子类父类低耦合
- 灵活性得到了保证
